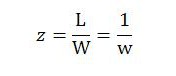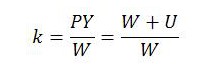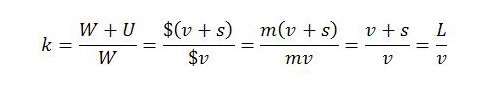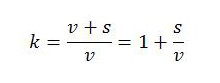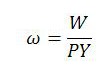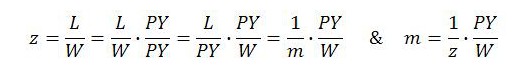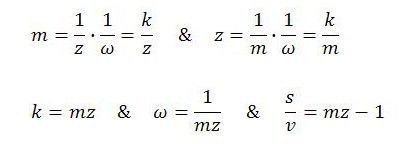The first post in this series distinguished between three types of macro measures: ‘monetary’, ‘real use-value’ and ‘real labor-time’ magnitudes. Under simplifying assumptions, the post spelled out basic connections between these different kinds of variables. The same assumptions are retained in this post to highlight a connection between the aggregate markup (Kalecki), the rate of surplus value (Marx), value of the currency (MMT) and the monetary expression of labor time (MELT).

The assumptions are:

1. a pure private closed economy;
2. no fixed capital;
3. all labor is simple and paid the same wage;
4. the level of productivity is taken as given;
5. the general price level does not change.

It should be mentioned that the macro-level connections identified under these assumptions — though basically valid — will be subject to modification later in the series when various assumptions are dropped. Not only this, but different interpretations of Marx would require different modifications to be made. Interpretative differences largely come down to: (i) the way constant and variable capital are defined; and (ii) whether value determination is considered simultaneous or temporal. It is too early to get into these issues. Suffice to say for now that, in this series, constant capital and variable capital will be defined as the amounts actually paid for inputs and labor power, with value determined temporally. At the moment, all that matters is the definition of variable capital. The reason for this, apart from the simplifying assumptions, is that attention is being confined just to the new value added in the production period. Any interpretation that understands variable capital to be the amount paid for labor power will generate the same results. (For those familiar with the Marxist literature, this is true of the New Interpretation and all single-system interpretations, whether simultaneist or temporal.)

Despite the simplifying assumptions, the results presented at this early stage are still of interest. A lot of short-run macroeconomic models employ a similar set of assumptions. For example, the Keynesian income-expenditure model in its simplest form assumes a private closed economy with productive capacity, productivity and the price level all taken as given. Just as the present focus is on new value added, other short-run models often center on a measure of society’s net product or income.

Okay, enough of the qualifications and caveats …

Consider the start of a new production period. Suppose it is known, based on data from the previous period, that the MELT (or monetary expression of labor time) is $20/hour. This means that each hour of simple labor in the previous period happened to create $20 of value. Under the assumptions of a constant price level and productivity, the MELT will be the same in the upcoming period. This is because the MELT, under present assumptions, is equal to the price level multiplied by the level of productivity. That is, m = Pρ. Since P and ρ are constant by assumption, so is the MELT.

To initiate production, capitalists outlay $c of constant capital for means of production and $v of variable capital to employ workers for the period.

The monetary outlay for constant capital is necessary to acquire the raw materials used up in production. More generally, if we hadn’t assumed away fixed capital, the capitalists would also have to cover wear and tear on plant and equipment. During the labor process, workers transfer preexisting value from the elements of constant capital to the final product. According to single-system interpretations, the monetary amount $c is calculated using the prices of the elements of constant capital. Input quantities are multiplied by these prices to arrive at the monetary outlay for constant capital.

The amount of money outlaid as variable capital will be equivalent to the total money wages W and other costs of employing workers advanced by capitalists. Here, it is assumed that the other costs of employment are factored into the wage bill. The advance is an autonomous expenditure, financed either out of past savings or a bank loan.

It is useful at this point to work out the value of the currency as defined in MMT. The value of the currency will be denoted by z. It can be calculated as the level of employment L, expressed in terms of simple labor, divided by the wage bill. Equivalently, it can be calculated as the reciprocal of the minimum hourly wage w. With all labor assumed simple, the minimum wage is the same as the average wage:

Defined in this way, the value of the currency is the amount of labor time that must be performed to obtain a unit of the currency. Conversely, and equivalently, it is the amount of labor power that capitalists can command with a unit of the currency.

For instance, if the wage rate is $10/hour, the value of the currency will be 0.1 hours/dollar. With an outlay for variable capital amounting to $100 billion, capitalists will be able to pay for (0.1 hours/dollar) x ($100 billion) = 10 billion hours of labor power.

The next question is, how much value will be created as a result of this 10 billion hours of labor power? Well, the MELT is $20/hour, so total new value will be mL = $200 billion. Under our present simplifying assumptions, this is nominal GDP. It is clear also that workers have produced surplus value of $s = mL – $v = $100 billion.

The surplus value generated in a single hour by an individual worker performing simple socially necessary labor will equal the difference between the MELT and the hourly wage: $s/hour = m – w. Equivalently, this surplus value will equal the difference between the MELT and the reciprocal of the value of the currency: $s/hour = m – 1/z.

Marx’s concept of surplus value can be related to Kalecki’s notion of the markup. One version of the markup k is expressed:

In this expression, Y is real income and U is total money profits prior to their distribution into various elements (retained earnings, interest, dividends, rent, etc.). The markup shows the extent to which nominal income exceeds money wages, expressed as a ratio.

From a Marxist perspective, Kalecki does not provide a fully satisfying explanation of what determines the markup. He does provide an explanation in terms of physical output (a real use-value explanation) and also a monetary explanation. In physical terms, he points out that when commodities are produced for capitalists, as either investment goods or capitalist consumption goods, they are unavailable for worker consumption. This leaves a physical surplus for capitalists. In monetary terms, he points out that when capitalists outlay money on the production of investment goods and capitalist consumption goods, the prices paid in aggregate for final output will exceed the wages of workers, leaving a monetary surplus that can be distributed among capitalists themselves. But Kalecki does not offer a real labor-time explanation.

A Marxist is inclined to ask, what actually determines the size of the markup? Or, what is its real basis? From a Marxist perspective, it is not enough to say that the real basis is the surplus of physical commodities. This leaves open the question of what ensures this physical surplus translates into surplus value. Similarly, from a Marxist perspective, it is not enough to say that the surplus value is ensured by capitalists’ monetary expenditures. This leaves open the question of what determines the size, in real terms, of those monetary expenditures. Marx wanted to explain the real basis of surplus value.

Although Kalecki does not address this question, his notion of the markup does provide an organizing framework capable of accommodating Marx’s answer. As a ratio of monetary variables, Kalecki’s notion of the markup can be translated directly into a ratio of Marxian monetary magnitudes and then converted into labor-time measures.

In labor-time terms, the markup is revealed to be a ratio between total living labor performed in the period and necessary labor time (the amount of labor time required to offset wages). The more workers are coerced into production beyond this point, the larger the markup.

It now becomes evident that there is an intricate connection between the markup and Marx’s concept of the rate of surplus value. The rate of surplus value – sometimes called the ‘rate of exploitation’ – is the ratio between surplus value and variable capital, or s/v. It indicates the proportions in which newly created value are distributed between workers and capitalists:

In our numerical example, the rate of surplus value s/v is equal to 1. This is because workers perform half their labor time to reproduce the equivalent of variable capital (5 billion hours) and the other half to create surplus value for capitalists (5 billion hours). The expression above shows that Kalecki’s markup must equal 2. It is simply the rate of surplus value plus 1. The meaning is that the net value product (= v + s) is twice as large as variable capital (v), or equivalently that nominal GDP (= $v + $s) is double the capitalists’ monetary outlay on variable capital ($v).

So, although Kalecki does not explain the markup in terms of surplus labor, there is an openness in his formulation that makes it compatible with Marx’s theory. It is possible to reconcile the two views as mutually consistent and, if desired, incorporate the insights of both into an explanation of the markup.

It is perhaps not surprising that there is a close connection between the markup and the rate of surplus value considering that the markup happens to be the reciprocal of the wage share ω in nominal income:

Not only does this make the markup and the nominal wage share inseparable concepts, but it also indicates that they are closely connected with the two other macro measures we have already discussed. These are the value of the currency z and the MELT m. The connection is evident once it is recognized that, under present assumptions, both z and m are proportional to the markup or, equivalently, proportional to the reciprocal of the nominal wage share. (With our assumptions, m = PY/L, as discussed in the previous post.)

Since the markup (or reciprocal of the nominal wage share) enters these expressions for z and m, all four macro concepts, as well as the rate of surplus value, are closely connected:

In the present context, if we know the wage rate, then we know z. It is simply the reciprocal of the wage rate. With the MELT given – because the price level and productivity are assumed constant – we also know the markup and rate of surplus value.

To illustrate the above relationships between k, ω, m, z and s/v, again consider one hour of socially necessary labor performed by a single worker. Suppose, as before, that the MELT is $20/hour and that the value of the currency is 0.1 hours/dollar, implying an hourly wage rate of $10/hour. In that single hour, m = $20 of value will be created, which of course is the monetary equivalent of the one hour of labor. Of that, $v = $10 will be paid to the worker, leaving the other $10 as surplus value for capitalists. Multiplying the MELT by the value of the currency gives 2, which is the markup as conceived by Kalecki. Taking the reciprocal gives the nominal wage share of 0.5. This indicates that workers receive half the new value produced in the period. Subtracting 1 from the markup gives the rate of surplus value.

Finally, relating back to the conversion factors between monetary, use-value and labor-time variables identified in the previous post:

In closing, I will note that while the precise nature of the connections presented in this and the previous post will be subject to modification as assumptions are discarded, a close connection between the markup, MELT and value of the currency will remain. It will also be seen later that the core connection between monetary, real use-value and real labor-time measures (m = Pρ) will re-emerge in a temporal setting in a form that, though modified, still resembles the one considered in these preliminary posts.