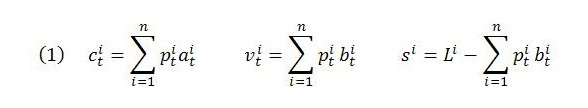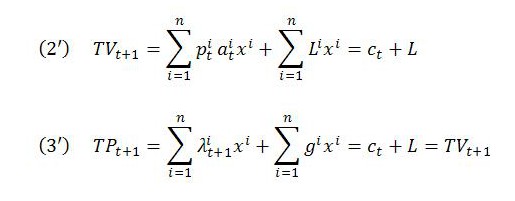Differences in interpreting Marx, as we have seen, tend to come down to three key questions. The first concerns how the value of labor power is understood. This will affect the treatment of variable capital. Is its value determined by the labor embodied in wage goods or the prices of those goods? The second question concerns the value of the means of production. This pertains to constant capital. Is the value of constant capital determined by the labor embodied in inputs or the amounts paid for them? The third question concerns whether value and price determination should be considered simultaneous or temporal. It was pointed out in the previous post that Marx’s aggregate equalities stand or fall with our answers to the first two questions. His equalities hold provided constant and variable capital are assumed to depend upon the prices of inputs and wage goods rather than the labor embodied in them. This approach is taken by all single-system interpretations, whether temporal or simultaneist. For the purposes of this post, adopting any of these interpretations would have been fine. However, the choice between temporality and simultaneity will sometimes be relevant later in the series. By way of background, the present post specifically introduces the temporal single-system interpretation (TSSI).

Although the focus here will be on the TSSI, my inclination in this series is only to commit to a particular interpretation over others when such a choice is unavoidable. We can think of the exercise in terms of relaxing assumptions. For some purposes – for instance, when envisaging something akin to a short-run macro model, as was done in parts 1 and 2 of this series – all that matters is the determination of variable capital. This is because, in parts 1 and 2, we applied fairly restrictive assumptions, appropriate to a short-run focus, and confined our attention to new value added in a period. In that context, as long as the value of labor power was defined in terms of the prices paid for wage goods, there was no need to choose between any of the numerous well known interpretations that take that approach. There will still be times later in the series when the discussion will apply under this broader range of interpretations. For arguments that require Marx’s aggregate equalities to hold, it becomes necessary, as already mentioned, also to define the value of the means of production in terms of input prices. This is the purview of the present post. Later, in contexts where temporality is an issue, it will be necessary to commit specifically to the TSSI if the arguments presented are to be considered valid.

The motive for proceeding in this way is to bring out the degree of compatibility between different interpretations rather than only emphasizing their points of difference. It also means that readers who disagree with the TSSI – or single-system interpretations more generally – can still hopefully get something out of the exercise. A Marx-MMT synthesis would not necessarily have to involve one particular interpretation of Marx over others, notwithstanding the TSSI influence on this series.

Having acknowledged the influence, I need to stress that the viewpoint expressed in this series may in quite a few respects differ from that of the proponents of the TSSI. They themselves have differences among themselves. Statements of their position are provided in Freeman and Carchedi (1996), Freeman, Kliman and Wells (2004) and Kliman (2007). (Full references are provided at the end of the post.) The first of these books includes individual chapters from leading developers of the approach. The second book features dialogue between proponents of the TSSI and authors offering opposing viewpoints. The third book explains the TSSI and summarizes the history of the debate on Marx’s theory of value from that perspective.

There is one more point that I should make clear from the outset. In this post, it is assumed that a unit of the currency always represents the same amount of socially necessary labor. In other words, the MELT is assumed constant. This assumption will be dropped, at times, later in the series. Temporality modifies the formula for the MELT and this has ramifications for the macro relationships considered in parts 1 and 2 of the series.

 
Value and price determination in the TSSI

As the name suggests, the TSSI is above all ‘temporal’ and ‘single-system’. Being temporal, it views economic processes as dynamic and non-equilibrium in nature. Prices and values are determined sequentially, with outputs and output prices of one period functioning as inputs and input prices of the next. Being single-system, the TSSI views prices and values as mutually determinative. There is not, in this perspective, one set of forces determining values and another separate set of forces determining prices. Values and prices are thought to determine each other, but in a sequential rather than simultaneous fashion.

In what follows, I have decided to avoid matrix algebra. This makes the presentation a little more cumbersome than would otherwise be the case. The concern is that matrix algebra might be inaccessible to some, even though it is actually easier than the alternatives once you have been exposed to it. Apart from the present post, I don’t envisage employing algebra again in this series beyond an elementary level. The algebra seems necessary here to make clear the way in which the TSSI is able to replicate Marx’s aggregate equalities. For those who absolutely loathe algebra, hopefully you can still read around it okay. The next post will be almost entirely words.

For those who actually enjoy algebra, a more sophisticated presentation of the material is provided in Kliman and McGlone (1999). An introductory treatment that mostly mimics a section of Kliman and McGlone’s paper is provided in a previous post. The post employs matrix algebra and works through a numerical illustration.

Notation. Unit, sectoral and aggregate magnitudes. We will begin by considering the unit price and unit value of a commodity produced in sector i, which is one of n sectors that each produce a single commodity. A superscript i is attached to variables that relate to an individual sector. The absence of a superscript indicates an aggregate variable applying to the economy as a whole. For instance, sⁱ is the surplus value associated with a single unit of sector i’s output. The total amount of surplus value created in sector i is equal to the per-unit surplus value sⁱ multiplied by the physical quantity of gross output xⁱ produced in the sector, or sⁱxⁱ. The amount of surplus value s created in the economy as a whole will equal the sum of all the surplus value created at the sectoral level; that is, s = Σ_isⁱxⁱ.

Time subscripts. The production period commences at time t and ends when commodities are ready to be exchanged at time t+1. In the TSSI, the prices of inputs and wage goods that determine the values of variable and constant capital are those prevailing at time t. They carry a t subscript. The values and prices of output, in contrast, will be those prevailing at time t+1. These have a t+1 subscript. Processes that occur over the entire period (meaning period t) from time t to time t+1 should, strictly speaking, have the subscript t,t+1. Such processes include the living labor performed, the profit and surplus value generated, rates of profit and the physical output produced over the period. To make the exposition a little less clunky, these processes will have no subscript. But it will be best to keep in mind that the meaning of no time subscript is actually t,t+1.

Value and price determination. At time t, capitalists combine means of production and living labor to produce output ready for sale at time t+1. The necessary outlay for used up means of production (i.e. constant capital) depends on the prices p_t of inputs prevailing at time t and the amounts a_t of the commodities used as inputs. Similarly, the necessary outlay for variable capital depends on the going wage rate at time t, which will purchase for workers a basket b_t of wage goods at period t prices.

To produce one unit of its commodity, sector i requires the amounts of constant and variable capital shown in (1). Labor performed in excess of the amount paid for variable capital will generate surplus value for capitalists:

In words, constant capital is calculated by multiplying each input’s price by its quantity and summing the resulting products. Since many commodities won’t be used as inputs for sector i’s commodity, these input quantities will be zero. Likewise for variable capital, we multiply the price of each wage good by its quantity and sum the results. Again, any commodity that is not consumed by workers – i.e. that is not a wage good – will have a quantity of zero.

The sum of cⁱ_t and vⁱ_t is the ‘cost price’ and, in single-system approaches, enters both the value and price of the individual commodity. The commodity’s output value λⁱ_t+1 at time t+1 will equal cost price plus surplus value. That is, λⁱ_t+1 = cⁱ_t + vⁱ_t + sⁱ. Its output price pⁱ_t+1 will equal cost price plus profit. That is, pⁱ_t+1 = cⁱ_t + vⁱ_t + πⁱ. So, the only difference between the value and price of the commodity is that the latter includes an amount gⁱ = πⁱ – sⁱ. This means that the output price can be written pⁱ_t+1 = cⁱ_t + vⁱ_t + sⁱ + gⁱ. Notice in (1), though, that vⁱ_t + sⁱ = Lⁱ. Therefore, we can simplify the expressions for the commodity’s output value and price to λⁱ_t+1 = cⁱ_t + Lⁱ and pⁱ_t+1 = cⁱ_t + Lⁱ + gⁱ.

The expression for constant capital in (1) can be substituted into these formulas for the value and price of the new commodity.

The mutual interdependence between value and price has two aspects under the TSSI.

One aspect relates to output values. As shown in (2), output values at time t+1 depend on period t input prices. This interdependency relates specifically to constant capital. The value of variable capital does not directly affect the value or price of the commodity because new value created equals the living labor performed, irrespective of its division into variable capital and surplus value. The definition of variable capital is still important, though, because by affecting distribution, it affects the amount of surplus value and the rate of profit.

The second aspect of value-price interdependency operates at the aggregate level and follows from Marx’s key argument that value cannot be created or lost in exchange. To be clear, this is to be understood in real terms, correcting for any inflation. (Recall, the MELT is assumed constant in this post.) What a buyer gains by buying cheaply the seller loses and so forth. This means that the price-value differences for individual commodities sum to zero in aggregate.

Multiplying the sectoral price-value deviations gⁱ by gross physical output levels xⁱ and summing gives the total deviation g of prices from values for the economy as a whole.

To see the significance of this, we can calculate total value TV_t+1 and total price TP_t+1 for the economy as a whole. Total value is calculated by multiplying each commodity’s value in (2) by its output quantity and summing the resulting products together. Total price is calculated in the same way except to apply the procedure to each commodity’s price in (3) rather than value:

This confirms that the first of Marx’s aggregate equalities holds under the TSSI. Namely, total value equals total price.

Rearranging (3′) shows that in aggregate:

This says that, apart from any inflation, the value added in price terms for the economy as a whole (total price minus constant capital) equals the amount of living labor performed. This accords with Marx’s view that all new value is created by living labor.

Marx’s other aggregate equalities also hold under the TSSI. Specifically, total surplus value equals total profit and the price rate of profit r equals the value rate of profit σ. Both rates of profit are calculated in relation to total capital K_t.

In the TSSI, the determination of the average rate of profit as a ratio of aggregate value magnitudes is prior to the determination of prices. The determination is prior not only logically but temporally. The average rate of profit will be the same irrespective of how prices actually distribute the surplus value already created in production.

 
Discussion. The economic processes represented by the above algebra can be summed up as follows. Each period begins with purchases of – or the application of – inputs that were produced in an earlier period and whose prices form part of the given data for the new period. There is no reason to suppose that these prices are at equilibrium levels, and in general they won’t be. Nor, in general, will prices equal values, as has already been discussed earlier in the series. But once input prices are established, it will be these prices, rather than input values, that determine the amount that must be paid to acquire the inputs necessary for production.

Since it is the price, not value, of the inputs that determines the outlay necessary for production of the commodity, the difference between the price and value of the inputs “is incorporated into the value of the new commodity as an antecedent element” (Marx 1971, p. 167). In the passage from which this brief quote comes (reproduced at greater length in the next part of this series), Marx appears to make explicit that, in his view, and consistent with the single-system position, it is input prices, not values, that enter into the values of final commodities. (Similar statements can be found elsewhere in Marx’s writings, as will also be illustrated in the next post).

A major attraction of the TSSI is that it replicates Marx’s theoretical results in a straightforward manner. In the case of Marx’s equalities, the same is true of all single-system interpretations. If in attempting to interpret a theory we can’t replicate its results, it might cause us to ponder whether we have actually interpreted the theory as it was intended to be interpreted. This is especially so if there are interpretations – single-system interpretations, in the present context – that do replicate the results without difficulty. This is an argument put forward strongly by Andrew Kliman (2007). Kliman credits the interpretative principle to George Stigler.

Being able to replicate Marx’s theoretical results does not, of course, mean that the theory is necessarily worthwhile. It would be possible, for instance, to take the view that an interpretation that fails to replicate Marx’s results might nonetheless provide the basis for a better theory. What replication does establish is internal consistency. Marx’s key results can be shown – and have been shown – to follow logically from explicitly stated premises.

Even so, a few questions may spring to mind. For one, it might be wondered why it would make sense to define the values of constant and variable capital in the single-system way. For another, it might be asked if this is an interpretation that accords with what Marx wrote on the issue. We saw a tiny snippet above of one passage that appears to lend support to the single-system view, but the question calls for a closer look. Needless to say, an even more fundamental question, which relates to all Marxist approaches to value, concerns the rationale for considering labor to be the sole creator of new value. The next part of this series offers some thoughts on the first two questions. The third, more fundamental question is left for later (UPDATE: see Musing on Labor as the Source of Value).

 
References

Freeman, A. and Carchedi, G. (eds.) (1996), Marx and Non-Equilibrium Economics, Cheltenham: Edward Elgar.

Freeman, A., Kliman, A. and Wells, J. (eds.) (2004), The New Value Controversy and the Foundations of Economics, Cheltenham: Edward Elgar.

Kliman, A. (2007), Reclaiming Marx’s “Capital”: A Refutation of the Myth of Inconsistency, Lanham: Lexington.

Kliman, A. and McGlone, T. (1999), ‘A Temporal Single-system Interpretation of Marx’s Value Theory’, Review of Political Economy, Vol. 11, No. 1, pp. 33-59.

Marx, K. (1971), Theories of Surplus Value, Vol. III, Moscow: Progress Publishers.