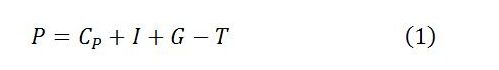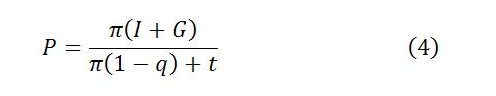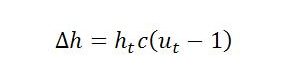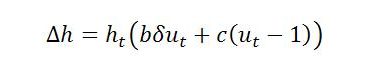Regular readers may have noticed that I am interested, among other topics, in demand-led growth theories as explanations of capitalist growth performance. In the following discussion, I borrow very liberally from two approaches in this theoretical tradition, without remaining completely true to either of them. One is Kalecki’s approach, especially as outlined in his 1954 work, Theory of Economic Dynamics. Following Kalecki, the current discussion treats the long run simply as a sequence of short runs without any independent existence of its own. Lagged effects of private investment generate cycles. Capitalist growth is considered to be dependent upon ‘external markets’, by which is meant sources of demand that are external to the domestic private sector. Here, for simplicity, government is taken to be the only external source of demand. (For an open economy, exports are another important example of demand that is external to the domestic private sector.)
The second body of work that strongly influences what follows is the ‘supermultiplier’ theory adopted by some proponents of the surplus approach, following Serrano’s 1995 contribution, The Sraffian Supermultiplier. Following that approach, and unlike Kalecki, it is assumed that private investment is purely induced. In particular, when total demand is persistently strong and, as a consequence, rates of capacity utilization high, firms are assumed to install additional plant and equipment in an attempt to adjust capacity to demand. Consistent with the supermultiplier theory, the determiner of the average long-term rate of economic growth is considered to be the behavior of a particular type of demand that is (i) exogenous of the circular flow of income and (ii) does not directly create private-sector capacity. This can be called ‘non-capacity-generating autonomous demand’, denoted Z. For simplicity again, government spending is taken to be the only demand of this type, though in reality autonomous private consumption expenditure, business expenditure on research and development, and exports also belong to this category.
The present discussion in relation to the supermultiplier approach and Kalecki
The only notable differences between the model to be presented here and the models developed in the surplus approach are the explicit consideration of cycles and the adoption of Kalecki’s conception of the long run as simply a sequence of short runs. Cycles are included by assuming that private investment responds to the rate of utilization (as in supermultiplier analyses) as well as to changes in that rate in the recent past. In the supermultiplier approach, cyclical effects (though sometimes present, depending on the assumed degree of responsiveness of investment to deviations in the utilization rate) are usually set aside in order to focus on certain characteristics of long-run growth behavior.
At first glance, linking private investment to the rate of utilization might seem to depart significantly from Kalecki’s approach. The conception of investment behavior, however, is similar. Kalecki argued that investment depends upon both the level of economic activity and the change in that level in the recent past. His proxies for these factors were total profit and the change in total profit (in his simplest model, the level of investment and the change in investment). In fact, the rate of utilization and the level of profit – and also the actual rate of profit – all rise and fall in lock-step over the business cycle when distribution and technology are taken as given, as they will be in the present discussion.
Key characteristics of the model
Two basic characteristics of the model to be sketched out can be summed up from the outset. Inside resource limits – which is an important proviso – and assuming a given marginal propensity to leak from the circular flow of income:
- the long-term average rate of economic growth is determined by the growth rate of non-capacity-generating autonomous demand (Z); and
- cyclical fluctuations around the long-term growth rate are generated by induced investment behavior.
Limitations of the present discussion
The model in the simple form presented here is preliminary in nature. It might be possible to build upon it to consider other issues. Among these are: (a) consequences of trends in the sectoral balances or income distribution for the financial stability of the growth process; and (b) demand-led growth in relation to Marx’s ‘law of the tendential fall in the rate of profit’.
The cycles considered in this post are not the kind that cause serious problems for capitalism. Basically, they are just a result, long ago emphasized by Harrod, of investment having an immediate impact on demand but only a delayed effect on productive capacity. This causes investment behavior to accentuate both expansions and contractions in activity. But provided there is sufficient “space” for investment to have its temporary demand effects without causing either runaway hyperinflation or debilitating deflation, these cycles are not a systemic threat. In practice, the necessary space does usually exist, because firms intentionally operate with planned margins of spare capacity, which enables them to adjust output to demand at more or less given prices over a fairly wide range of output.
The roots of more serious problems with the capitalist system – such as those that caused the Great Depression or the more recent global financial crisis and Great Recession – will be something deeper than this Harrodian instability. The roots might lie in a tendency toward financially unsustainable private credit creation (perhaps considered from the standpoint of the sectoral balances, as in (a) above). Or it might be linked to Marx’s tendency for the rate of profit to fall (as in (b)). Or there might be some other factor of central importance. It might be possible to extend the present model to illustrate some of these possibilities.
In its present, limited form, the model basically depicts a demand-led growth process as it might play out prior to factors such as (a) or (b) making themselves felt.
An elementary model of cyclical growth
Simplifying assumptions:
- A closed economy with government and private sectors.
- The economy is always inside resource limits with an excess labor supply.
- All private consumption expenditure is induced. Workers spend all their wages. Capitalists consume a constant fraction of profit.
- Taxes are purely endogenous.
- Government spending is exogenous.
- Private investment, though exogenous of the current-period circular flow of income, is induced by the level of economic activity and changes in that level in the recent past.
- A constant profit share in income (‘exogenous distribution’).
- A constant normal output to capital ratio (‘fixed technology’).
Every one of these assumptions could be relaxed. For instance, we would need to relax assumptions 7 and 8 in order to consider Marx’s law of the tendential fall in the rate of profit. And we would want to include the external sector when considering a national economy rather than the global economy as a whole.
Kalecki’s basic framework
Since I have borrowed so heavily from Kalecki, his notation and characterization of the economy is adopted, but the same could be achieved with the Keynesian income-expenditure model (an example is outlined in a previous post, linked to below).
Kalecki shows that total (after-tax) profit P is equal to capitalist consumption expenditure CP plus private investment I plus government spending G minus taxes T:
Here, for simplicity, capitalists are assumed to consume a constant fraction q of total after-tax profit:
Taxes equal the marginal propensity to tax t multiplied by total before-tax income:
Multiplying and dividing the right-hand side of (3) by total profit P, and noting that P/Y = π is the share of after-tax profit in total before-tax income, enables us to express taxes in terms of P:
Here, π = 1 – t – ω, where ω is the share of after-tax wages in total before-tax income.
Substituting (2) and (3′) into (1) gives total profit as a multiple of those expenditures that are exogenous of the current-period circular flow of income (i.e. investment and government spending):
Total income Y can now be found by multiplying and dividing the left-hand side of (4) by Y, recalling that P/Y is the profit share π, and solving for Y:
This is a simple multiplier relation in which total equilibrium income is a multiple of exogenous planned expenditure (I + G) and the size of the multiplier depends on the profit share, capitalists’ marginal propensity to consume and the marginal propensity to tax.
For present purposes, it is sufficient just to denote the denominator of (5) by α. This makes α the marginal propensity to leak to taxes and saving, and 1/α the multiplier.
An investment rule
The task now is to settle on a decision rule for private gross investment I. It will be supposed that two factors induce variations in the rate of investment in period t+1:
1. The rate of utilization in period t. If the rate of utilization in the previous period exceeded the normal rate, investment will be encouraged in the new period. If utilization is below normal, investment will be discouraged. If the actual utilization rate equals the normal rate, investment will grow at the rate at which the economy as a whole is expected to grow.
2. The change in the rate of utilization between times t–0.5 and t+0.5. A positive rate of change is assumed to encourage investment; a negative rate of change to discourage it.
In a recent post, a supermultiplier model was considered in which firms behaved in such a way that the investment share in income, h = I/Y, followed a rule of the form:
The number ‘1’ in this expression represents normal utilization (i.e. un is defined to equal one). This behavioral rule says that the investment share in income rises whenever the rate of utilization exceeds normal (ut > 1). This accounts for factor 1 above (the rate of utilization) but not factor 2 (the change in that rate). To incorporate factor 2, the above decision rule can be modified:
Here, δ is the central difference operator such that δut = ut+0.5 – ut–0.5. That is, δut is the change in the utilization rate from time t–0.5 to time t+0.5. The parameters b and c are assumed positive and constant. They measure the strength of the response of the investment share to changes in the utilization rate (factor 2) and the utilization rate itself (factor 1), respectively.
Noting that Δh = ht+1 – ht, ht = It/Yt and ht+1 = It+1/Yt+1, we can rearrange the preceding expression to obtain an investment function:
This expresses gross private investment of period t+1 as a function of income over the same period. A difficulty, mirrored in the “real world”, is that income of period t+1 is unknown at the time investments of that period are made. Further complicating matters, income will itself depend on investment of the same period.
At first blush, it might seem that we can get around this by linking income of period t+1 to income of period t via the growth rate of period t, denoted gt (where period t begins at time t and ends at time t+1):
But, of course, gt is also unknown until Yt+1 is known. In reality, investment can only be guided by the expected output of period t+1, which will depend in turn on the expected rate of growth:
The ‘e’ superscripts denote expectations. The investment function becomes:
It is therefore necessary to make an assumption about the way expectations are formed. If expectations are formed adaptively, the simplest assumption is that firm’s expect this period’s growth rate to equal the previous period’s growth rate:
This investment rule shall be adopted in the ensuing discussion. Equivalently, investment of period t+1 can be expressed as a function of investment of period t (making use of the fact that ht = It/Yt):
The investment behavior described by (7) differs from Kalecki’s treatment in two ways that have already been anticipated. First, investment in (7) is entirely induced, whereas Kalecki included an exogenous, trend component. The point of the present exercise is to illustrate how autonomous expenditure might induce investment. At minimum, all we need for that purpose is the inclusion of one component of non-capacity-generating autonomous demand. All other spending in the model can be induced. I chose government spending because government, especially if a currency issuer, is the actor most able to maintain a particular rate of growth in its own spending. Of course, the growth in its spending still needs to be in sensible relation to the economy’s real capacity to adjust to demand in a manner that is not excessively inflationary.
A second difference is that the investment equation is defined in terms of the rate of utilization rather than profit and the change in profit. This is not a significant departure from Kalecki in the present context because under simplifying assumptions 7 and 8 the rate of utilization, actual profit and the rate of profit all move in lock-step. However, once we wish to consider alterations in distribution and technology, there is a debate to be had over whether it is demand or profit or the rate of profit that drives growth.
Private investment behavior
By construction, the actual rate of utilization u = Y/Yn can exceed 1 (the normal rate un) up to some absolute physical maximum umax. This maximum rate of utilization will be associated with the maximum possible actual output Ymax (> Yn).
The basic idea is that firms intentionally adjust their capacity to a level that most of the time will not be fully utilized (Yn < Ymax) so that they will be able to expand output to meet unanticipated peaks in demand rather than lose market share to competitors. Firms try to set capacity such that the average level of demand is supplied when Y = Yn < Ymax, which in turn implies that u = un = 1 < umax.
Firms are assumed to adjust capacity to demand only slowly, and with reference to changes in the average level of demand. In terms of the investment rule depicted in (7), the parameters b and c must be small. (It is not discussed here, but dynamic stability requires this.) In other words, it is assumed that firms, in formulating their investment plans, do not jump at shadows, reacting to every temporary fluctuation in demand, but rather attempt to take a longer view. The whole point of having planned spare margins of capacity is to accommodate unanticipated peaks in demand through a more intensive utilization of existing capacity.
Below the absolute maximum capacity, firms are assumed to adjust output to demand at given prices. The prices themselves will be set with reference to what each firm expects will be the average or ‘normal’ rate of capacity utilization. Actual utilization will fluctuate around its normal rate, usually below the absolute maximum utilization. If, in rare instances, demand temporarily exceeds the maximum possible output, there will be ‘pure inflation’ (in which prices rise to inflate away the difference), non-price rationing, or some combination of the two.
Numerical example
Suppose the parameters and starting values of key variables (denoted by subscript 0) are as shown below.
Under these settings, the economy evolves through time in a cyclical fashion with an upward trend, where the trend reflects the behavior of government spending. The long-term average growth rates of private investment, productive capacity, normal output and actual output are the same as those described in Sraffian supermultiplier models of demand-led growth. A simple example of such a model is outlined in a previous post, Demand-Led Growth – Government Spending and the Investment Share. It is easy to modify all the growth equations presented in that earlier post to include the influence of changes in the rate of utilization (δut). The modifications affect the growth trajectory but not the long-run average rate of growth to which the economy tends. In the earlier post, this growth behavior was described in fairly formal, algebraic terms. In what follows, the representation of the growth process is less formal with a reliance on diagrams generated from spreadsheet analysis. The numerical example errs on the side of depicting a fairly volatile economy, to illustrate the model’s demand-led growth process in an obvious fashion. Specifically, the values for the investment parameters b and c have been chosen so that, although dynamic stability is achieved, the cycles are quite pronounced. Choosing smaller values for b and c would mean smaller cycles and more rapid convergence to the long-run average growth rates.
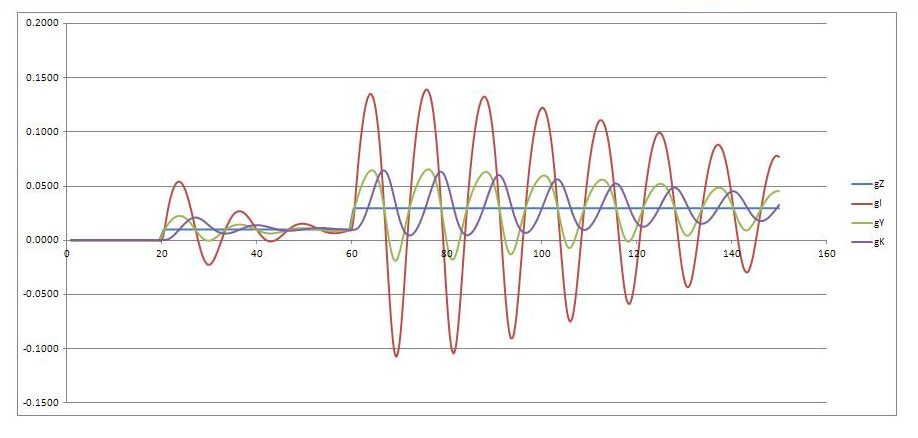
In our highly stylized scenario, depicted in the above figure, the economy is imagined to be stationary for twenty periods, with private investment behavior and productive capacity reconciled to a constant level of government spending. At time t = 20, the government steps up its level of spending by 1 percent each period, and maintains this growth rate in government spending for forty periods. At time t = 60, the growth rate of government spending is stepped up further to 3 percent and maintained at that rate for the remainder of the time horizon under consideration.
When the growth rate of government spending is increased (represented in the diagram by a steepening of the purple line), the effect is to boost the growth rate of total demand. Firms respond, at given prices, by expanding output through a more intensive utilization of existing capacity. The trajectory of actual output (black line) steepens, with actual output rising above normal output (blue line) and closer to the maximum possible output (red line). With the rate of utilization above normal and the most recent change in the utilization rate positive, private investment in plant and equipment is accelerated, in accordance with the investment rule (expression (7)). The extra investment adds immediately to demand and, after a delay, also to productive capacity. As a consequence, there is a lagged steepening in the trajectories of both normal output (blue line) and maximum possible output (red line). Investment, at this stage, is growing faster than the economy as a whole, which in turn is growing faster than government spending. The capacity effects of investment eventually cause a reversal of the cycle, at first acting upon the change in the rate of utilization, which switches from positive to negative, and then pushing the rate of utilization itself below normal. This discourages investment, which now grows less rapidly than both the economy as a whole and government spending. However, so long as government continues to step up its spending at a constant rate, this again causes the rate of utilization to mount, and the cycle repeats. From period 20 onwards, the economy’s overall trend is upward because the growth rate of government spending is positive.
Inside resource limits, a more rapid growth in government spending tends to lift the share of private investment in income (I/Y) and reduce the share of government spending (G/Y, or more generally, Z/Y). The reason for this is explained at length in the earlier post linked to above. Basically, the economy’s transition to a higher growth rate in response to stronger government spending requires private investment to grow faster on average than the economy as a whole (and faster than government spending) over the transition period. As a result, the level of investment rises relative to income, whereas the level of government spending (or, in a more general model, Z) falls relative to income. For the present numerical example, the behavior of the investment share, the government spending share and the utilization rate are depicted below.
The investment share cycles up to a higher percentage of income; the government spending share does the opposite. If the growth rate of government spending remained constant for long enough, the rate of utilization would eventually restore itself to normal, but during the transition phase utilization would be above normal on average.
The next diagram shows the effect of government stepping up the growth rate of its spending. It is not obvious from inspection, but over the entire time horizon, the average growth rate of investment (2.28 percent) exceeds that of total demand and income (2.13 percent) which, in turn, exceeds the average growth rate of government spending (2.07 percent). This enables capacity eventually to catch up to demand.
It was noted earlier that a simple form of adaptive expectations has been assumed. This was purely for simplicity. Given the assumptions of the model, the precise manner in which expectations are formed, and whether they are ‘adaptive’ or ‘rational’, will not affect the long-term average growth rate to which the economy converges. This is because the long-run growth rate of the economy is determined, within the model, solely by the growth rate of the non-capacity generating autonomous expenditures Z (in this simplest version of the model, by the growth rate of government spending).
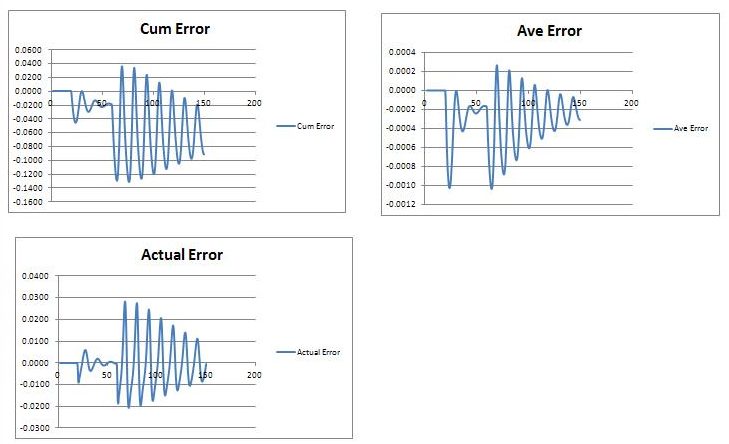
What will vary under different expectational assumptions is the path through which the economy approaches its long-run, demand-determined growth rate. With adaptive expectations, a long-lasting increase in the growth rate of Z will cause systematic underestimation of the economy’s actual growth rate during the transitional path to a higher long-run growth rate, with the errors gradually getting smaller until, if given sufficient time, vanishing. In contrast, under rational expectations, errors would be randomly distributed with mean zero until convergence occurred.
The systematic underestimation of the economy’s growth rate that has been assumed in the simple model is evident in the cumulative error in expectations, which is negative. This means, of course, that the average error is also negative. Even so, the actual error would eventually converge on zero if government spending behavior (or, more generally, the behavior of Z) remained the same for a sufficiently long time.
In short, within the model, the long-term average rate of economic growth is not affected by the manner in which expectations are formed, provided investment is assumed (as it has been here) to be responsive to variations in the rate of utilization. Granted this investment response, the growth rates of actual and normal output (and productive capacity) tend to adjust gradually to that of government spending (or Z).
Within the model, if a ‘fully-adjusted position’ were ever reached, in which productive capacity happened to be fully reconciled to total demand, then actual output, private investment, the capital stock, normal output and the maximum possible output would all grow at the same rate as government spending (or Z) until government happened to alter its spending behavior.
Needless to say, such an eventuality is purely hypothetical. A capitalist economy will never reach such a fully-adjusted position, even if government behaved in this way, because (i) there are other components of Z not subject to tight governmental control and (ii) the marginal propensity to leak to taxes and saving, though likely to be quite stable for various institutional reasons, will in reality move around somewhat over time (its constancy in the model is a simplifying assumption), causing the size of the expenditure multiplier likewise to vary somewhat over time.
The key characteristic of this and similar models is that the economy, at any point in time, is notionally tending toward a long-term average growth rate that is determined by the behavior of Z, whatever that behavior may be.