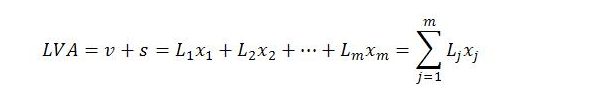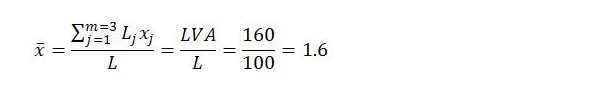Value, in Marxist theory, is an amount of abstract labor that is measured in hours of simple labor or a monetary equivalent. Marx argued that complex labor is reducible, for the purposes of commodity production and exchange, to amounts of simple labor. Qualitatively, complex and simple labor are the same. Both count as abstract labor, and so create value. But, quantitatively, complex labor creates value at a faster rate than simple labor.
This distinction between simple and complex labor complicates Marxian analysis. It remains open to debate whether the complications extend to the macro level. Marxian macro analysis – especially empirical analysis – would be made considerably easier if the value implications of labor complexity could be treated at the aggregate level in much the same way as the effects of variations in average productivity. The latter have no direct impact on the amount of value created in aggregate. Their direct impacts on value creation are only felt at the micro level.
As convenient as it would be for aggregate value creation to be unaffected by labor complexity, it seems, following the logic of Marx’s theory, that this will not be the case. For Marx, productivity pertains to concrete labor and the production of use values; labor complexity pertains to abstract labor and the creation of value. Variations in productivity do have a direct macro impact. It is just that the impact is on the aggregate production of use values rather than value. In contrast, variations in labor complexity, since they relate to abstract labor, would seem to affect the aggregate creation of value.
Unfortunately, the matter is not easily resolved by consulting Marx’s writings. Marx wrote very little on the reduction of complex to simple labor and does not appear to have distinguished explicitly the value effects, if any, that may operate at the level of aggregates. In the opening chapter of the first volume of Capital, he observes that a “commodity may be the outcome of the most complicated labour, but through its value it is posited as equal to the product of simple labour. … The various proportions in which different kinds of labour are reduced to simple labour as their unit of measurement are established by a social process that goes on behind the backs of the producers”. But rather than elaborating in any detail on the nature of this reduction, he merely adds:
In the interests of simplification, we shall henceforth view every form of labour-power directly as simple labour-power; by this we shall simply be saving ourselves the trouble of making the reduction. (Capital, Vol. 1, Penguin, 1976, p. 135)
Apparently the distinction and its implications were clear to Marx. The way to operationalize the concepts involved may not always seem quite so obvious to his readers. The amount of debate on the topic, since that time, perhaps attests to this. Even so, I think that the distinction itself is clear and conceptually useful, despite the extra difficulties it may create for empirical macro analysis.
The focus, in what follows, is on the macro implications of Marx’s distinction between simple and complex labor. The discussion is organized as follows. First, in suggesting a possible interpretation of Marx’s conception of labor complexity, two aspects that seem especially open to different understandings are considered. One concerns the appropriate definition of simple labor. The other concerns the contrasting macro implications of labor complexity and average productivity for the rate of value creation. These sections are followed by a simple numerical example, aimed at illustrating the significance of labor complexity at the aggregate level under the suggested interpretation. It is assumed, for the purposes of the example, that the complexity of different labor is known. In practice, this will not be the case. The post closes with a consideration of two ways in which the issue might be approached.
Simple labor as both an average and a base level
According to Marx,
the value of a commodity represents human labour pure and simple, the expenditure of human labour in general. … It is the expenditure of simple labour-power, i.e. of the labour-power possessed in his bodily organism by every ordinary man, on the average, without being developed in any special way. Simple average labour, it is true, varies in character in different countries and at different cultural epochs, but in a particular society it is given. More complex labour counts only as intensified, or rather multiplied simple labour, so that a smaller quantity of complex labour is considered equal to a larger quantity of simple labour. (p. 135)
One possible difficulty in interpreting Marx’s argument concerns whether simple labor should be understood as an average kind of labor, a base level, or in some sense both. Since an hour of complex labor creates more value than simple labor, it appears that simple labor does serve as a base level. Specifically, one hour of simple labor equals one hour of value, and so could be said to have a base-level complexity of 1. An hour of labor that counts as x hours of value would then have complexity of x (where x > 1). But, by the same token, since simple labor draws only upon labor power that is possessed, on average, by all workers, it is also an average. Entering into the determination of this average will be labor power that has not been developed “in any special way”. In today’s societies, for instance, a role that requires the worker to have completed no more than basic schooling might be considered to involve simple labor, whereas a role that requires the worker to have undergone specialized training would involve complex labor. Of all the roles requiring the application of only simple labor power, some will be performed with greater proficiency than the average, and so more than meet the standard of simple labor, while others will be performed with less proficiency than the average and fall short of the standard of simple labor. But the average performance in all these roles will constitute simple labor.
In a sense, then, simple labor can be regarded as both a base level and an average. This raises the question of how to draw the line between simple labor – the expenditure of labor power that is not developed in any special way – and complex labor. Only labor power that has not been developed in any special way enters into the social average that, when expended, constitutes simple labor. Perhaps the simplest choice would be to identify simple labor with the labor performed on average by minimum-wage workers. But other choices are also possible.
To represent the issues involved, suppose in general that there are m levels of labor power, ranked by labor complexity. The complexity of labor power in category j (j = 1,…,m) can be denoted xj. Let j = 1 refer to the category of simple labor. The complexity of simple labor is x1 = 1. For all other categories, labor complexity exceeds 1 (i.e. xj > 1 for j > 1). The dimensions of xj are hours of simple labor per raw hour of employment (or, equivalently, hours of simple labor per hour of concrete labor). Using this terminology, labor of complexity xj contributes the equivalent of xj hours of simple labor per raw hour of employment. In other words, the complexity of level j labor indicates the amount of value it creates in one raw hour of employment.
In labor-time terms, the new value created in a given period, or ‘labor value added’ (LVA), will be an amount of simple labor, with hours of complex labor reduced to equivalent amounts of simple labor. Let L denote total raw hours of employment and Lj the raw hours of category j employment. New value will be
where v is variable capital and s surplus value. Average labor complexity for the economy as a whole will be:
This implies:
If this interpretation of Marx’s argument is accepted, labor complexity has an impact on value creation, including at the aggregate level. As expression (1) indicates, the amount of new value created in a period will be the product of two components, namely total raw hours of employment (L) and average labor complexity (x bar). In the special case where all labor is simple, average labor complexity equals 1 and labor value added is determined solely by the total raw hours of employment (that is, LVA = L). This makes theoretical analysis much easier and so is often assumed as an analytical device. But since, in general, some labor is complex, it is not always appropriate to abstract from the issue.
Labor complexity and average productivity
Another point on which interpretations can differ concerns how Marx’s distinction between simple and complex labor relates to his analysis of productivity. Marx held that
The same labour, therefore, performed for the same length of time, always yields the same amount of value, independently of any variations in productivity. (p. 137)
From a macroeconomic standpoint, this is a very useful (and analytically powerful) implication of Marx’s theory. It means that the aggregate level of productive employment, reduced to hours of simple labor, measures the new value (LVA) created in the period. If the level of productive employment (again, reduced to hours of simple labor) were to remain unchanged from one period to the next, the amount of value created would be the same for both periods.
If so, it is evident that average productivity and labor complexity are distinct concepts with different implications for the aggregate economy. On the basis of Marx’s statement on page 137, a change in average productivity has no direct impact on value creation at the aggregate level. In contrast, a change in labor complexity will directly affect value creation because, as stated on page 135, an hour of complex labor counts as a multiple of simple labor, implying that it will create more value than an hour of simple labor.
As already alluded to, this difference in the macro impacts of labor complexity and average productivity is grounded in Marx’s distinction between abstract and concrete labor. Labor complexity is a characteristic of abstract labor, whereas average productivity is a characteristic of concrete labor. Abstract labor creates value; concrete labor produces use values. Variations in productivity have no impact on the total amount of value created for a given level of employment because productivity, being a characteristic of concrete labor, has its macro impact on the amount of use values produced rather than the amount of value created. In contrast, labor complexity, being a characteristic of abstract labor, has implications for value creation, including at the macro level.
Marx’s statement that an hour of simple labor always creates the same value irrespective of variations in productivity is part of a longer passage that clearly distinguishes concrete labor and use-value production from abstract labor and value creation:
By ‘productivity’ of course, we always mean the productivity of concrete useful labour; in reality this determines only the degree of effectiveness of productive activity directed towards a given purpose within a given period of time. Useful labour becomes, therefore, a more or less abundant source of products in direct proportion as its productivity rises or falls. As against this, however, variations in productivity have no impact whatever on the labour itself represented in value. As productivity is an attribute of labour in its concrete useful form, it naturally ceases to have any bearing on that labour as soon as we abstract from its concrete useful form. The same labour, therefore, performed for the same length of time, always yields the same amount of value, independently of any variations in productivity. But it provides different quantities of use-values during equal periods of time; more, if productivity rises; fewer, if it falls. …
On the one hand, all labour is an expenditure of human labour-power, in the physiological sense, and it is in this quality of being equal, or abstract, human labour that it forms the value of commodities. On the other hand, all labour is an expenditure of human labour-power in a particular form and with a definite aim, and it is in this quality of being concrete useful labour that it produces use-values. (pp. 136-7)
The macro implications of productivity improvements and rising labor complexity are therefore different. If the average complexity of labor changes, the same raw hours of productive employment (measured without regard to labor complexity) will represent a different amount of simple labor and so result in different labor value added. However, if productivity improves while raw hours of employment and average labor complexity remain unchanged, labor value added will be unaffected.
Numerical example
Consider a period in which the workers engaged in commodity production perform a total of 100 raw hours of labor. Of this total productive employment, imagine that there are three categories of employment, corresponding to different levels of labor complexity. It can be assumed that 60 hours involve simple labor, 20 hours involve labor that is twice as complex as simple labor, and the remaining 20 hours involve labor that is three times as complex as simple labor.
On the basis of these numbers, there are m = 3 categories of employment, with L1 = 60, L2 = 20, L3 = 20, x1 = 1, x2 = 2, and x3 = 3. Plugging these numbers into the expression for new value created in the period gives:
New value for the period amounts to 160 hours of simple labor. Average labor complexity for the economy as a whole can be calculated as:
In terms of expression (1),
On the suggested interpretation of Marx’s treatment of labor complexity, the average degree of labor complexity (x bar) clearly has an impact on value creation. If all labor were simple, the average complexity of labor would be 1, and new value only 100. But with average labor complexity of 1.6, new value is 160. As anticipated, higher labor complexity translates into greater value creation, including for the economy as a whole.
In contrast, higher productivity has no direct effect on value creation at the macro level. This is clear from the expression for labor value added (LVA) which, being the product of raw hours of employment and average labor complexity, is not directly affected by productivity. In terms of the example, new value will be 160 hours of simple labor irrespective of movements in average productivity. So long as raw hours of productive employment remain the same from one period to the next, the value created can only change if there is a change in average labor complexity.
If the example is modified slightly such that workers in the third category perform labor of complexity x3 = 4 rather than x3 = 3, and all other details are left unchanged, then new value will increase to
which will reflect an increase in average labor complexity to
Now, as a consequence of the change in labor complexity, it is highly likely that average productivity has also changed. But since productivity pertains to concrete labor and use values, as opposed to abstract labor and value, any such change in productivity will be reflected in the rate of production of use values and not in the rate of creation of value. As before, so long as the average complexity of labor remains unchanged at 1.8, any subsequent variations in productivity will affect real output but have no direct impact on value creation at the macro level.
There can also be a reduction in average labor complexity. This is quite likely to be accompanied by rising, rather than falling, productivity. This can happen when skills that were special become prevalent in society, such as when their instruction is introduced into elementary education. It can also happen as a result of deskilling. For instance, basic document formatting that can be performed by most workers today using a word processor once required skilled labor. Working from the initial numbers in the numerical example, if half the raw hours of category 2 employment were replaced by roles requiring only simple labor, new value would decline from 160 to 150 and average labor complexity would fall to 1.5.
Practical difficulties and two possible responses
It has been noted that if the interpretation of Marx’s argument outlined above is appropriate, it makes life more difficult for the macroeconomist attempting to integrate Marxian value considerations into empirical analysis. Reconsider expression (1), which is the main implication of the suggested interpretation:
Labor value added (LVA) is difficult to estimate because of the presence of labor complexity, which is not directly observable.
The need to take account of labor complexity also complicates the determination of the ‘monetary expression of labor time’ (MELT) when this is defined as the money value created per hour of simple labor. The MELT is an important analytical device for moving between monetary variables and labor-time variables. Under special assumptions (most notably, when the levels of productivity and prices are taken as given), the MELT (m) can be expressed as:
Here, MVA is ‘monetary value added’. It is the sum of variable capital and surplus value measured in monetary terms (i.e. MVA = $v + $s). If labor value added (LVA = v + s) were directly observable, the MELT could be calculated simply by dividing monetary value added by labor value added. But whenever average labor complexity is greater than one (meaning whenever some labor is complex), labor value added cannot be directly observed. As the expression shows, the MELT is also affected by average labor complexity, and so is equally difficult to approximate.
What is much easier to determine is the product of m and x bar, which is sometimes referred to as the ‘monetary expression of concrete labor time’ (MECLT):
This measure indicates the money value that is created per raw hour of employment or, as the name suggests, the money value created per hour of concrete labor.
Empirical work sometimes focuses on the MECLT rather than the MELT. This is understandable considering the difficulties involved in estimating labor complexity. But without an estimate of labor value added, it remains unclear whether the behavior of the MECLT reflects movements in labor complexity, and hence variations in the rate of real value creation, or instead merely reflects nominal changes in the MELT.
Of course, it is one thing to prefer measures that are based on labor value added rather than raw hours of labor time, but this begs the question of how labor complexity is to be estimated. For some forms of short-run macro analysis, it may be reasonable to assume that average labor complexity remains approximately stable over the short period in question. If so, movements in total raw hours of productive employment (L) will serve as a good indicator of the behavior of labor value added (LVA) and it will be appropriate to interpret a change in the MECLT as a change in the MELT. In a longer run context, in which the average complexity of labor will have more time to change, perhaps a case can be made that there are tendencies operating to mitigate the issue. But, at least for some purposes, it seems desirable to have a reliable method of estimating labor complexity.
There appear to be at least two possible approaches to the problem. One approach might look to a possible uniformity of the rates of surplus value applying to different sectors and categories of labor with a view to interpreting wage rates as an indicator of labor complexity. Another approach might be to estimate labor complexity by examining the time it takes to replicate the results of different categories of labor.
Approach 1: Wages and rates of surplus value
In the special case where the average rate of surplus value happens to apply uniformly throughout the economy, labor complexity will be accurately reflected in wage relativities. By identifying, for example, simple labor with minimum-wage labor, average labor complexity will equal the average money wage divided by the minimum wage. This will be true no matter what the rate of surplus value, so long as it applies uniformly.
In practice, rates of surplus value are presumably not strictly uniform, but if they are approximately so, it would probably be hard to do better than make this assumption in empirical analysis. The accuracy of the method will obviously depend on the extent to which sectoral rates of surplus value (and also the rates of surplus value applying to different skill categories of labor) deviate from the social average. There might be a case for arguing that, under competitive conditions, rates of surplus value tend to equalize, and then making appropriate corrections for sectors or categories of labor where this is thought not to be the case due to monopolistic elements.
Marx, himself, did suggest that rates of surplus value (also called ‘rates of exploitation’) will tend to equalize (for instance on p. 275 of volume 3 of Capital). In relating this “law” to labor complexity, he wrote:
Other distinctions, for instance in the level of wages, depend to a large measure on the distinction between simple and complex labour that was mentioned already in the first chapter of Volume 1, p.135, and although they make the lot of the workers in different spheres of production very unequal, they in no way affect the degree of exploitation of labour in these various spheres. If the work of a goldsmith is paid at a higher rate than that of a day-labourer, for example, the former’s surplus labour also produces a correspondingly greater surplus-value than does that of the latter. (Capital, Vol. 3, Penguin, 1981, p. 241)
To the extent that competition pushes wages to the levels that reflect labor complexity, there will be a tendency for rates of surplus value to converge to the average rate. A paper by Cogliano provides an interpretation of Marx’s logic along these lines. The result will be a long-run tendency rather than something that holds at a given point in time, but if operative would probably justify an assumption of equal rates of surplus value for the purposes of empirical analysis.
Rates of surplus value are significant because, together with wages, they indicate the value created in an hour of labor. Of the value xj created per raw hour of employment of a category j worker, a fraction will replace the advance made per hour in variable capital, which will amount to the hourly wage (inclusive of benefits) wj. The remainder will represent the surplus value appropriated per hour which, given knowledge of variable capital and the rate of surplus value, can be calculated as $v(s/v) = $s. But unless rates of surplus value in all sectors (i = 1,…,n) and labor categories (j = 1,…,m) can be considered uniform (si/vi = sj/vj = s/v for all i and j), or at least roughly so, it will be necessary to approximate each sector’s rate of surplus value and possibly also the rate applying to each category of labor if there is reason to think that some categories of labor are systematically more exploited than others.
This is a difficult task. It is much harder to estimate sectoral rates of surplus value than the average rate. At the macro level, monetary value added (MVA) is, in principle, observable (allowing for decisions about what to include in productive activity). This is true, at least, under the ‘new’ and ‘single-system’ interpretations of Marx’s theory. However, at the micro level, monetary value added is not directly observable, even in principle. The observable magnitudes are price rather than value measures and these, in general, do not coincide at the sectoral and firm levels. If a sector’s monetary value added did happen to be observable, a sector’s rate of surplus value could be measured directly from the sector’s monetary value added and money wages. But, unfortunately, this is not the case. The bottom line is that, somewhere along the line in this approach, assumptions will need to be made about the behavior of sectoral rates of surplus value relative to the average rate. Whether this is problematic depends on how closely sectoral rates of surplus value mirror the average rate. Since it may not be possible to determine the answer to this question empirically with much certainty, adoption of the assumption needs to have a solid justification in theory, which seems possible along the lines indicated by Marx in the passage quoted above.
Approach 2: Time required to replicate the results of complex labor
Another approach to analyzing labor complexity might be to estimate the time it takes to replicate the results of different categories of labor, although any benefit of adopting this vantage point might be more conceptual than practical, for a reason to be discussed.
A previous post raised the idea that labor is the sole source of commodity value because what is being valued are the results of human effort expended in production. In some sense, the idea goes back at least as far as Adam Smith. To the extent that human effort is involved in the production of a commodity, something is created that cannot be replicated (or reproduced) without exertion of that level of effort. For Marx, as for the classical political economists, the value of a commodity is the time required to reproduce it. Certainly Marx emphasized, more than his predecessors, the social nature of the processes involved. It is not just time, but socially necessary time. The human effort must be directed toward the needs of commodity production and exerted with the average degree of intensity (productivity) for it to count as an hour of simple, socially necessary labor. And to count as complex labor – a multiple of simple labor – the human effort must also be performed with special skills that are not currently within the capacities of most members of the community.
The results of simple labor are easier to replicate than the results of complex labor because simple labor draws only upon skills that are prevalent in the given society. An hour of complex labor will create more value than an hour of simple labor because of the greater difficulty of replicating the effort that goes in to that labor. To take an extreme example by way of illustration, suppose the needs of commodity production require, among its many roles, one and only one worker to possess a special skill that takes seven years to develop. Imagine that one worker has been trained for the one available role and, as a consequence, there is no shortage of the complex labor power in question so long as this one worker persists in the role. But suppose the worker decides s/he would prefer to quit the role to take up a new job involving only simple labor. Temporarily, it will be impossible to replicate the results that were achieved by the worker, and it will remain impossible until another worker has learned the skill, which currently involves a seven-year learning process. This difficulty of replication appears to be what makes the complex labor more value creating than simple labor. With the worker now in a different role, total raw hours of employment perhaps remain unchanged. Even so, labor value added for the economy as a whole will have decreased, because the worker who before was performing complex labor is now in a role that any number of others, biding their time in the reserve army of the unemployed, will be equipped to perform if s/he ever needs to be replaced.
In reality, there are usually queues of workers willing and able to accept different kinds of jobs, so the difficulty of replicating effort will not be as extreme as in the example just considered. But there is still a need for an ongoing training of new generations of skilled workers to replace those entering retirement or moving on to other roles. Accordingly, replication of the results of complex labor will require the social reproduction of workers who are capable of performing it so long as the roles are not deskilled and the labor is not made simple through introduction of the relevant training into basic education.
More generally, whether the labor performed is simple or complex, the capitalist ends up with output that cannot be matched other than through the expenditure – by somebody – of similar effort. The capitalist owns the result of the effort. This result cannot be competed away to nothing, because it cannot be replicated without putting in the socially necessary effort to do so. Meanwhile, the worker tends to get paid an hourly wage that reflects the cost of reproducing the capacity to perform the role for another hour. Provided the worker creates more value (exerts more effort) than is required to reproduce the worker’s capacity to perform labor, surplus value remains for the capitalist.
As a tendency, capitalists will only purchase labor power – whether simple or complex – if the rate of surplus value applying to that labor is expected to be sufficient to return the general rate of profit. Other factors remaining equal, if complex labor were not more creative of value than simple labor, it would not be profitable for a capitalist to purchase complex labor power. If complex labor merely created value at the same rate as simple labor, it would make more sense for the capitalist to purchase simple labor power because of its lower cost of reproduction. But since the results of complex labor can be replicated only with greater effort than is true of the results of simple labor, complex labor does create more value and so can be sufficiently profitable for the capitalist.
On the basis of these considerations, it may be possible to estimate the complexity of different categories of labor power through an analysis of the time required to replicate the results of the labor. But this seems a much harder task than would be necessary, under the first approach, if rates of surplus value could be considered approximately uniform. The main difficulty with assessing the time to replication of different kinds of labor outcomes is that adding up the hours will require some preliminary assumptions about the complexity of the various labor processes involved. Without making some initial estimates of the labor complexity of different categories of labor, based perhaps on a consideration of long-run wage relativities – which will implicitly amount to adopting the first approach under an assumption of uniform rates of surplus value – there will be no solid basis for the time estimates. But this introduces a circular reasoning that will hamper the approach as a practical method, although some kind of iterative procedure might still be workable.
With these considerations in mind, the first approach based on wages and an assumption about rates of surplus value seems to offer the best hope for empirical purposes. The main benefit of the second line of reasoning, centered on the time to replication of labor outcomes, may be in the intuitive understanding it offers on why labor is the source of value and, more specifically, why complex labor might have implications for value creation, including at the macro level.
Concluding remark
If the interpretation of Marx’s conception of labor complexity outlined above is appropriate, variations in labor complexity will directly affect aggregate value creation. To be clear, it is perhaps worth emphasizing that this macro effect is for a given level of total productive employment, measured in raw hours (or hours of concrete labor). That is, if labor complexity changes while the level of productive employment remains the same, value added will change. However, if some of the labor that goes into generating the special skills applied in commodity production is unproductive, and an increase in average labor complexity tends to be associated with an increase in the employment of unproductive labor as part of the reproduction process of complex labor power, then there may be a tendency for the level of productive employment to decline as labor complexity increases, other factors remaining equal. It would be nice if, roughly speaking, the two factors canceled each other out and the macro effects of labor complexity could be safely ignored.
Needless to say, there is also the question of the suggested interpretation’s appropriateness. If, contrary to the interpretation, labor complexity actually has no direct impact on aggregate value creation, we would be spared from a lot of complicating considerations. But it seems to me, primarily on the basis of Marx’s distinction between abstract and concrete labor, that the macro effects considered are in fact likely to apply.