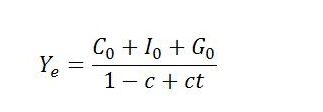In this and upcoming parts of the series, we will look in a little more detail at the ‘income-expenditure model’. The foundations of the model have been introduced in the previous two parts (here and here).
We have seen that, within the model, equilibrium output is determined by two main factors:
- the level of autonomous expenditure (denoted A);
- the marginal propensity to leak (denoted α).
The expenditure multiplier k is 1/α. Equilibrium output is a multiple of autonomous spending, kA.
By delving a little more deeply into the components of both A and α, the model can help us to explore various connections between government policy, private spending behavior, income distribution and other factors. To keep things relatively simple, for now a closed economy is considered. A closed economy is one that does not interact with any sector external to itself. The most important example is the global economy as a whole. In contrast, an open economy, such as an individual trading nation, does interact with an external sector. We will return to an open economy later in the series.
In a closed economy, we can distinguish between three main categories of spending: private consumption (C), private investment (I) and government spending (G). By accounting identity, total output and income (Y) equal total spending:
Y = C + I + G
We can also distinguish three main uses of income. As we saw in part 5, some income goes to taxes (T), some is consumed (C) and some is saved (S):
Y = C + S + T
If we set the right-hand sides of these two identities equal to each other (since they both equal Y), we find that:
I + G = S + T
Private investment and government spending are known as injections. An injection is an expenditure that is not made by (domestic) households and is autonomous of income. We have already seen in earlier parts that saving and taxes are leakages. So the last identity says that:
Total Injections = Total Leakages
Now, the expressions considered above are simply identities. In themselves, they do not say anything about behavior. The income-expenditure model combines identities with particular behavioral assumptions.
In the determination of equilibrium output, the focus is on planned spending, not actual spending (this distinction was discussed in part 17). The model makes certain assumptions about planned spending behavior.
Private consumption is considered to be largely induced by income, but there is also a role for autonomous private consumption. These assumptions are embodied in the following consumption function:
CP = C0 + c(Y – T)
This says that planned private consumption (CP) is positively related to disposable income (income Y minus taxes T). A ‘P’ subscript is used to represent planned variables.
C0 is autonomous consumption. A ‘0’ subscript indicates an autonomous variable. Autonomous consumption is unrelated to income.
Induced consumption is represented by the term c(Y – T). In this term, c is the marginal propensity to consume. It is the fraction of an additional dollar of disposable income that goes to consumption. The fraction is always between 0 and 1. Private consumption increases with disposable income because of the extra consumption this induces, represented by c(Y – T).
If we suppose that taxes T are simply a constant fraction t of income (that is, T = tY), the consumption function can be written:
CP = C0 + c(Y – tY)
The fraction t is known as the marginal propensity to tax.
All other categories of spending (the injections) are assumed to be autonomous of income: IP = I0 and GP = G0.
Equilibrium output is equal to the sum of planned expenditures (Y = CP + IP + GP). Substituting the expressions for each category of spending, we have:
Y = C0 + c(Y – tY) + I0 + G0
We can group together on the left-hand side all terms that involve Y, then factorize:
Y – cY + ctY = C0 + I0 + G0
(1 – c + ct)Y = C0 + I0 + G0
Solving for equilibrium output gives:
The ‘e’ subscript says that the level of income is consistent with equilibrium. The result accords with what we have observed in previous posts. In particular, equilibrium income is a multiple of the sum of autonomous expenditures C0, I0 and G0. The expenditure multiplier k is:
In the formulas for output and the multiplier, 1 – c + ct (= α) is the marginal propensity to leak. It is the fraction of an additional dollar of income that leaks to saving and taxes.
This is perhaps made clearer if we rewrite the expression, making use of the fact that the marginal propensity to save s = 1 – c. The expression can then be written s + (1 – s)t, which if expanded and re-factorized with s now taken as a common factor, can be written s(1 – t) + t. Since s is the fraction saved out of extra disposable income, s(1 – t) is the fraction saved out of extra income. So we have the fraction of extra income going to saving, s(1 – t), plus the fraction of extra income going to taxes, t. This hopefully makes clear that s(1 – t) + t, which is equivalent to 1 – c + ct, is the marginal propensity to leak out of income (α).
Another way of seeing this is to rewrite 1 – c + ct as 1 – c(1 – t). Since c is the fraction consumed out of an extra dollar of disposable income, c(1 – t) is the fraction consumed out of an extra dollar of income. Therefore, 1 – c(1 – t) is the fraction of an extra dollar of income that does not go to consumption. Any income that does not go to consumption goes to taxes and saving, which again makes clear that the term 1 – c + ct represents the marginal propensity to leak out of income.
As expected, we have reached the same basic conclusion that output depends upon autonomous expenditure and the marginal propensity to leak. However, we can now notice things that were not so obvious in our simpler version of the model.
One observation concerns distribution. The expenditure multiplier (k) is bigger when the marginal propensity to save (s = 1 – c) and the marginal propensity to tax (t) are small. Because high-income households tend to save a higher proportion of their income than low and middle-income households, the marginal propensity to save will tend to be smaller when the distribution of income is more equal. Accordingly, a more equal distribution of income implies a bigger expenditure multiplier (k). A given level of autonomous spending (A = C0 + I0 + G0) will result in a higher level of equilibrium income when there is greater equality of income.
We could also say more about the sectoral balances, but we will leave this till next time.